Gnuplotでwarped band のエネルギー面を 3D プロットする

　Si や Ge の価電子帯の等エネルギー面は球形ではなく，結晶軸の特定の方向が突出した形になっている．このようなエネルギー面は fluted surface あるいは warped surface と呼ばれている．もともとは価電子帯の準位をなす波動関数がp波の対称性を有していることからこのような異方性が出現している．

　具体的にどの程度の異方性であるのか，視覚的に見たいと思い，価電子帯のエネルギー面を3次元 (3D) で描画してみることにした． 3Dの描画ソフトとしては，時々簡単なグラフを描いているGnuplot (4.4) に 3次元描画機能があるので，Gnuplot を使うことにした．

　しかしながら，私はGnuplotを使いこなすほどにGnuplotを熟知しているわけではない．それで，まずネットで球に近い閉じた曲面を描画している例を探したが，ぴったりと当てはまるものがなかなか見つからない．球やドーナッツのような数式で記述できる閉じた3次元表面の描画例はあるのだが，数値計算結果のデータファイルを取り込んで閉曲面を描画している例は，相当時間を掛けて調べたつもりであったが，結局見当たらなかった．

　そこで仕方がないので，Gnuplot の使い方やマニュアルをネットで検索して読みながら， warped surface の3D 描画方法を自分で考えてみた．かなりの時間を掛けて，悪戦苦闘の末，一応メッシュで描いた3D像を不十分ながらもようやく作成することができた．苦労したので，その方法をメモしておこう．

　warped band のエネルギー \cal{E} は次式で表される．

(1)\hspace{8mm} {\cal{E}}=\frac{\hbar^2}{2m_0}\{Ak^2\pm[B^2k^4+C^2(k_x^2k_y^2+k_y^2k_z^2+k_z^2k_x^2)]^{1/2}\}

この式は比較的小さい波数 k で成り立つことが知られている [1]．ここでは {\cal{E}}=50~{\rm meV} 程度のエネルギーを有する面をGnuplot を用いて3Dで描きたいということである．（計算では \hbar^2/2m_0 を1， k を r ， k_x=x などとしている．）

　3D描画には splot を使う．データファイルは (x[i], y[j], z[i][j]) を3次元空間の点の座標とすると，

x[0] TAB y[0] TAB z[0][0] LF x[0] TAB y[1] TAB z[0][1] LF x[0] TAB y[2] TAB z[0][2] LF ... x[0] TAB y[N] TAB z[0][N] LF LF x[1] TAB y[0] TAB z[1][0] LF x[1] TAB y[1] TAB z[1][1] LF x[1] TAB y[2] TAB z[1][2] LF ... x[1] TAB y[N] TAB z[1][N] LF LF ... ... ... x[M] TAB y[0] TAB z[M][0] LF x[M] TAB y[1] TAB z[M][1] LF x[M] TAB y[2] TAB z[M][2] LF ... x[M] TAB y[N] TAB z[M][N] LF
となるように書式が決っている．これはxy面内(z=0)に (M+1) \times (N+1)の格子を考え，その格子点をz軸方向に曲面z(x,y)に射影して，その点のz座標をz[i][j]としていることを意味している．データファイルでの格子点の並びは，最初y軸に平行にN個 1列並んだところで空白行を入れて一括りにする．次の括りは最初の格子点の並びに平行にN個並べることになる．これを M 回繰り返す．括りに含まれる個数が同じでない場合，射影した格子点を結ぶ線は y軸方向にしか描かれず，x軸方向は線が引かれないので1括りの点の数は同じにしなければならない．

　ということは，Gnuplot での内部処理は，格子の最小単位の四角形を端のほうから次々に曲面上に描く作業をしているということに違いない．そういうことがわかる．それなら，最小単位となる四角形の頂点の座標が定義できさえすれば良いので， xy面内の格子点は必ずしも直線上に並んでいる必要はないはずである．そこで，簡単なデータファイルを作って試してみると，確かにその通りで， xy面内の格子点の並びが曲がっていてもギザキザでも3Dメッシュを描いてくれることがわかった．

　しかし，3次元空間の閉曲面をこの方法で，つまりxy平面上の格子を閉曲面に射影して上の書式のようなデータを作ることはできない．なぜなら，z座標が2価になったり，射影点が存在しない格子点が出てくるからである．

　それなら，閉曲面の上に直接(M+1) \times (N+1)の格子を描けばよい．もしこれが描ければその格子点の座標を上の書式で並べれば3D 描画ができる．しかし，これには次の2つの問題がある．

閉曲面を重なる部分がなくかつ完全に覆うような等価な（トポロジカルに）四角形の格子を描くことができない．

格子の最小単位には必ず三角形が入ってきてしまう．

まずはこれを解決しないといけない．

　四角形の格子で閉曲面を区切るには，迂回方法として，北極と南極に小さい穴を開けて，それ以外の部分を経度線と緯度線で区切って等価的な矩形の格子にすることができる．これでも良いのかもしれないが，何かごまかしているようで気持ちが悪い．それで極座標の方位角，極角を2次元面としてこの上に格子を描き，それを閉曲面に転写することを考えよう．これで解決したような気になるが，ちょっと考えると，北極，南極に接するところが，四角形ではなく三角形になってしまうことがわかる．やはり，三角形の問題は避けられない．

　Gnuplotが内部処理している内容を考えると，三角形のpelette を3次元の閉曲面に描画するのも，四角形を描画するのと本質的には差がないと考えられる．それなら，この三角形を，四角形で2つの頂点の座標がたまたま一致している場合とみなせば同じように処理してくれるのではないだろうか．そこで，また簡単なデータファイルを作って試してみると，問題なく描画してくれる．これなら問題ない．ということで問題は解決してしまった．残ったのは rの計算だけであるが，これは簡単なプログラムで計算できる．

　プログラムでは，まず\phi-\theta面で (M+1) \times (N+1)の格子を作り，各格子点で，

(2)\hspace{8mm} x=r \cos\phi\sin\theta

(3)\hspace{8mm} y= r\sin\phi\sin\theta

(4)\hspace{8mm} z= r\cos\theta

として，この x, yから r を求め z を求めている．こうして得られた一連のデータを用いて最初に示した書式に沿ってデータファイルを作れば良い．

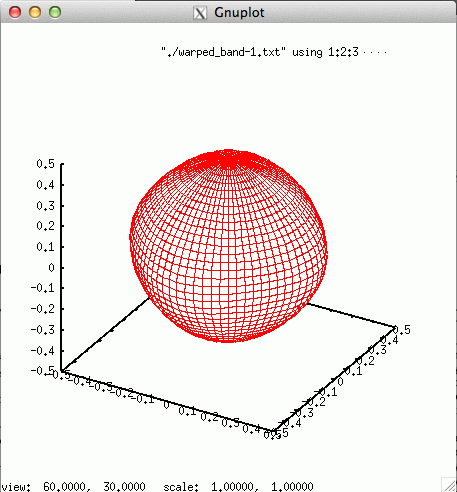
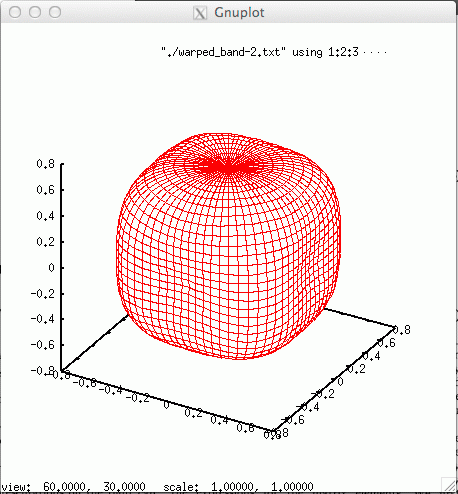
　以上のようにして作成したファイル warped_band-1.txtおよび warped_band-2.txtは次のように Gnuplot で処理すれば良い．ただし，前者は(1)で複号がプラス(light hole)，後者はマイナス(heavy hole)の場合である．

set ticslevel 0
set hidden3d
splot "warped_band-1.txt" using 1:2:3 with line ls 0

　その結果，次のような3Dのメッシュ表示が得られる．

　以上の画像は3Dメッシュ画像であって，色彩や濃淡による 3D画像ではない． Gnuplot ではpm3d というルーチンが用意されていて，それを用いると色彩に拠る3D表示が可能なはずであるが，このデータファイルに適用すると正しく表示されない．作成したデータファイルにまだ問題が残っていると考えられるが，それが何かはまだ明らかにはなっていない．

[1] G. Dresselhous, A. F. Kip, and C. Kittel, Phys. Rev. 98, 368 (1955).